| |
| Français / Português / Español / русский / 简 体中文 / 繁 體中文 / English / Nederlands / العربية |
第2章: 3次元エッシャーが3次元の図形を理解し ようとする2次元の生き物の冒険を語る. |
| 第1章へ | 第 3章へ |
1.語り手 |
|
エッ
シャー
(1898-1972)は,非常に優れた芸術家で,その作品は多くの数学者の興味をひきつけた.
彼の版画は,逆説的な世界,驚くべき対称性をもつタイル張り,無限の遠近法など,数学者を熱狂させるものをみせてくれるのである!こ
こ(フランス語)にある伝記を参照されたい.
版画の複製のコレクションについては公式サイト(英語)を参照されたい. バッハ (1685-1750)も数学者を魅了した芸術家のひとりである.バッハも驚くべき対称性を見せてくれる. ゲーデル (1906-1978)は論理学に革命を起こした数学者であるが,全体とその中の1つのものの間の対称性を研究した. 『バッハ,エッシャー,ゲーデル』という驚くべき本には,特別なこの3人をひとつにまとめる深い関係の研究が展開されている. |
|
エッシャーの最も有名な版画のひとつは『トカゲ』と名付けられてい る. ビデオの中では残念ながらあっという間に過ぎてしまっているから,ここで時間をかけてそれを鑑賞していただきたい. デッサン帳の一ページに平面的なトカゲが完全にはめ込まれているタイル張りが見える. |
|
これが平面的な世界のイメージである:このページに住むトカゲはこのページのことしか知らない. そして,彼らを取り囲んでいる空間は見えないのである. 我々はトカゲを見て,トカゲの世界が我々の空間の中にあるノートの一枚のページであることがわかるが,平面的なトカゲには見えないのである. このトカゲの一匹が幸運にも平面から脱出して我々の世界を訪れている:下の方でだんだん厚みを増し,本の上に 這い上がり,12面体の形の岬へ続く橋となっ ている定規を渡る. 再び下って平面世界の自分の位置に戻るまで,この新しい体験を新大陸を発見した探検家のように満喫している. この版画をみると,哲学的な思考へ導かれる: このトカゲに外の世界が見えないとすると,我々も同じ状況にあるのではないだろうか? 我々の『外の』世界,我々の感覚では感知できない世界は,存在しないのだろうか? ところで,この版画は哲学的な暗示に満ちている. ここにはプラトンが世界を形成すると考えた4元素が見える: コップの中の水,トカゲの鼻の穴から吐き出される空気,鉢の中の土,マッチ箱で表された火である.そして,12面体は『第5の元素』を暗示している … 「Job」というマークのタバコの巻紙は,聖書を意味するのだろうか? |
|
| All
M.C. Escher
Works © 2008 The M.C. Escher Company,the Netherlands. All rights reserved. www.mcescher.com Used with permission. |
|
この章の目的は,第4の次元への準備をすることである. 我々にとって超越的な第4の次元に向かうために,平面的なトカゲに3次元の物体を説明する方法を考えてみることから始める. 我々が天により選ばれたトカゲ(哲学者?数学者?)で,紙の上から出て12面体の上に登ることを許されていると想像してみよう. 我々は3次元の空間にいて,鉢,本,定規,12面体という物体を見ることができる.そして,我々の任務は,平面上にいて,そこから出られないためにそれを 見ることができない他のトカゲに,『物体を見せる』ことである. 2.『平らな国』 |
|
3.プラトンの立体我々の空間のどのような図形を平面的なトカゲに『見せれば』良いだろうか?花瓶や本を見せても良いのだが,哲 学的な暗示のために,プラトンの5つの立体を見せることにする. |
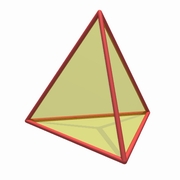 |
||||
| 正4面体 | 正8面体 | 立方体 | 正12面体 | 正20面体 |
|
これらの図形のうちには,立方体のようによく見かけるものもある.ときどき見かける4面体もある.そのほかの ものはあまり見かけないので,自然のなかでそれを見つけるには観察力が必要である. 例えば,20面体をとってみよう.12個の頂点があるが,その頂点を左の図のように切り取ってみよう.こうし て,20個の6角形と12個の5角形からなる 図形が得られる.これらの5角形は切り取られた12個の頂点から現われている.これが,サッカーボールだということがわかるだろう& hellip; |
|
この図形は,『多面体』,文字通り多くの面をもつものである!
我々の目的は,ここから多面体の複雑な理論に入っていくことではない.
我々は単に空間内の5つの美しい図形を選んで,それらをトカゲに見せてみたいだけである.
トカゲにサッカーボールがどんなものか説明したいだけである! 多面体にはたくさんの種類がある(もちろん無限にある). その中で5つだけが『正多面体』である. ここでも,この言葉の定義などに深入りはしない. しかし,この5つの正多面体のどれも同じ形の面を持っている(例えば,正12面体のすべての面は辺の長さが等しい正5角形である)こと,そしてどれも同じ 形の頂点を持っている(例えば,立方体の各頂点からちょうど3本の辺が出ている)ことがわかる. この性質が,我々がトカゲに見せようと思う5つの図形を(ほとんど)決定している. |
| 画像 | 名称 | 面の数 | 頂点の数 | 辺の数 (長さ L) |
表面積 | 体積 |
| 正4面体 | 4 | 4 | 6 | |||
| 正8面体 | 8 | 6 | 12 | |||
| 立方体 | 6 | 8 | 12 | |||
| 正12面体 | 12 | 20 | 30 | |||
| 正20面体 | 20 | 12 | 30 |
|
もっと多面体について知るためには,例えば,このフランス語のページやこ のページを見るとよい. 5つの正多面体の歴史,対称性などについてのもっと良く知るためにはこのフランス語のページや,このページを 見るとよい. これらの図形は,対称性の概念を象徴しているので,数学者は非常に好んでいる.残念ながら対称性についてはビデオではあまり説明されていない. 4.切り口 |
|
トカゲに正4面体を説明する 最初のアイデア は,それを切って見せることである. このアイデアは,古くからあるもので エドウィン・アボットも彼の本の中で何度も使っている. これは,断 層撮影(CT) という医療画像技術と同じようなものである.断層撮影では人体の断面を撮影し,このひとつながりの断面から3次元の体を再現するのである. 多面体が空間内を移動し,トカゲのいる平面と交わるとき,平面との交わりは多角形となる. 多面体が移動するにつれて,多角形が変化し,平面を横切ってしまうと消えてしまう. (多面体はマルセル・エイメの壁抜け男なのだろうか?) トカゲには,多角形しか見えないが,それが動き,変形するところは見える. 少し経験を積めば,(おそらく!)自分たちが空間の中で見ることはできない多面体がどのようなものかわかるに違いない. |
|
映像では,5つの正多面体が平面を横切り,変化する断面の多角形が示されている. これはあまり易しくない.その理由は断面は多面体が平面をどう横切るかに依っているからだ. 例えば,立方体がその面の一つが平面に平行だったとすると,何も不思議なことは起こらない: 断面は正方形である. しかし,立方体をその中心を通り,対角線に垂直な平面で切ると,切り口は…正6角形であるが,これはそれほど当たり前ではないだろ う?! 5つの多面体が平面を通過するのを観察した後で,エッシャーは練習をしてみようと言う. 多角形の切り口を見せて,通過しつつある多面体を当ててみなさいと言う. この練習がうまくいくように祈っているが,難しいことがわかるのだ. 断面を見るという方法には限界があるので,他の方法を見つけなければならない… 5.ステレオグラフ射影(立体射影)さて,2つ目のアイデアを説明しよう. 少し変な考え方と思われるかもしれないが,後で非常に有効な考え方であることがわかる(それは,我々が3次元の「平らな」空間にいる番になって,4次元に ある物体を選ばれた誰かが我々に説明するときにだ…). 我々は,球面を平面にステレオグラフ射影で写すこと,この射影は長さを変えること,しかしこの射影で地球の地理についての十分よくわかり,地球を平面上で 転がらせればもっと良くわかることを知っている… 我々は,同じこと,つまり5つの多面体を平面上で転がらせてステレオグラフ射影で平面に写そうとしてみる.問 題は立方体は丸くないから転がらせることはできないことだ! そこで,多面体を風船のように膨らませて丸くするのである. 球面の中に立方体を内接させてみよう. |
|
この章の後半ではこの方法が示されている. 最初に,すべてを見ることができる3次元の存在がみる図形を見せる. 多面体,膨らませた多面体,球面,トカゲのいる平面への射影が見える. それから,君達がトカゲの代わりになって,射影だけを見る番だ. どの多面体か当てるためには,君達の想像力が必要だとエッシャーは言う. この練習はあまり易しくはないが,断面を見る方法よりも易しいに違いない. この練習はあとで役に立つ.
これからは,君達は3次元にいる哀れな存在で,第4の次元を見ることはできないという立場にいることを,意識しなければならない!
第4の次元を見る才能をもった誰かが,彼が見えているものを君に見せる努力をするだろう.
彼も切り口を見せたり,射影を使ったりするだろう. |
| 第1章へ | 第 3章へ |