| 日本語 / русский / 繁 體中文 / Português / 简 体中文 / Français / Español / Nederlands / العربية |
Chapter 2 : Dimension threeM. C. Escher tells the adventures of two-dimensional creatures who are trying to imagine three-dimensional objects. |
| To chapter 1 | To chapter 3 |
1. The narrator |
|
M.C.
Escher (1898-1972) was an extraordinary artist
whose works attract the interest of many mathematicians. His
engravings show us paradoxical worlds, tilings with amazing symmetries
and infinite perspectives:
the sorts of things that really
fascinate mathematicians!
You can find a biography and a large
collection of reproductions of his engravings on the
official website . J. S. Bach (1685-1750) is another artist who fascinates mathematicians (among others!). He too presents us with astonishing symmetries. Kurt Gödel (1906-1978) was a mathematician who revolutionized logic, also exploiting symmetries between a whole entity and one of its parts. A remarkable book "Gôdel, Escher, Bach" explores the profound relationships between the works of these three exceptional figures. |
|
One of the most famous of Escher's engravings is entitled Reptiles. Let's take some time to admire it here, since unfortunately it goes by very quickly in the film. One one page of a sketchbook we see a tiling in which flat lizards fit together perfectly. |
|
This is the image of a flat world: the lizards who live in this page know only the page; they are ignorant of the space surrounding them. We see them, and we know that their flat world is only a page of a notebook lying in our space, but the flat lizards do not know this. One of these lizards finds a means of escaping the plane and visiting our world: we see him at the bottom gradually gaining thickness, climbing up on a book, using a drafting tool as a bridge leading to a promontory in the form of a dodecahedron, before going back down and resuming a position in his flat world, enriched by his new experience like an explorer who has just discovered a new continent. The engraving invites philosophical reflection: if these lizards are unaware of the existence of an exterior world around them, could we be in the same situation? Couldn't there be a world "exterior" to ours, to which our senses do not give us access? In fact, there are many philosophical allusions in this engraving. We see the four elements that according to Plato made up the world: water in the glass, air blowing out of the nostrils of the lizard, earth in the pot and fire suggested by the matchbox, and we even see the dodecahedron, which represented Plato's fifth element, the "quintessence"...Might the "Job" brand cigarette paper be a biblical allusion? |
|
| All
M.C. Escher
Works © 2008 The M.C. Escher Company,the Netherlands. All rights reserved. www.mcescher.com Used with permission. |
|
The purpose of this chapter is to prepare us for the fourth dimension. In order to envision a fourth dimension which envelops us, we will begin by imagining the strategies we might use to explain the existence of a third dimension to the flat lizards. We will imagine that we are this lizard chosen by heaven (the philosopher? the mathematician?) who had the privilege of being authorized to leave the page and climb onto a dodecahedron. We are in three-dimensional space, we see objects such as a pot, a book, a dodecahedron, and our mission is to "show" these objects to the other lizards who can't see them because they are confined to a plane that they cannot leave. 2. "Flatland" |
|
3. The Platonic SolidsWhat objects in our space shall we "show" to the flat lizards? We could show them a flowerpot or a book, but instead we will remain in a philosophical mode and show them the five Platonic solids. |
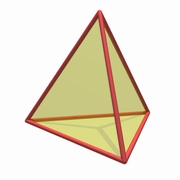 |
||||
| Tetrahedron | Octahedron | Cube | Dodecahedron | Icosahedron |
|
Some of these objects are very familiar to us, such as the cube. We occasionally encounter others such as the tetrahedron. Still others are quite rare, and you need to be very observant to find them in nature. For example, let's take the icosahedron, with its 12 vertices, and slice off each of the vertices as in the figure at left. We obtain an object consisting of 20 hexagons and 12 pentagons. The pentagons come from the 12 vertices which we sliced off, and correspond to the faces of a dodecahedron. You may recognize the final result as the pattern on a soccer ball... |
|
These objects are called polyhedra, which in Greek means literally that they have many faces! We do not intend here to go into a complicated theory of polyhedra. We simply want to choose five pretty objects in space and try to show them to the lizards, or perhaps somehow explain to a lizard what a soccer ball is. There are many polyhedra (an infinite number, in fact) but only five of them are regular. Here again, we don't want to enter into the details of the definition of this word, but just observe that for each of these five regular polyhedra all of the faces are of the same type (for example, all of the faces of the dodecahedron are regular pentagons, all of whose edges have the same length), and that all of the vertices are of the same type (for example, there are exactly three edges going out of each vertex of a cube). These properties are enough (almost) to characterize the five objects that we want to show to the lizards. |
| Image | Name | Faces | Vertices | Edges (length L) |
Surface | Volume |
| Tetrahedron | 4 | 4 | 6 | |||
| Octahedron | 8 | 6 | 12 | |||
| Cube | 6 | 8 | 12 | |||
| Dodecahedron | 12 | 20 | 30 | |||
| Icosahedron | 20 | 12 | 30 |
|
To learn more about polyhedra,
you can consult this page, and to learn much more about the
five regular polyhedra, their history and their symmetries, you can
consult this page.
These objects are among the objects most revered by mathematicians
because they symbolize the concept of symmetry, which is unfortunately
not described in the film. 4. Sections |
|
A first idea of how to explain to the lizards what a tetrahedron is, is to cut it in slices. This idea is very old, and Edwin Abbott uses it often in his book. This is pretty much the idea used in tomography, a technique of medical imagery which consists of examining the human body slice by slice and then reconstructing a 3-dimensional image from the successive cross-sections. When a polyhedron moves in space and encounters the lizards' plane, the intersection with this plane is a polygon. When the polyhedron moves, the polygon deforms, and eventually disappears when the polyhedron has finished passing through the plane (assuming polyhedrons can pass through walls like the "passe-muraille" of Marcel Aymé!). The lizards see only the polygons, but they see them in a dynamic way: they can watch how they deform. With a little experience they can (perhaps) eventually gain an intuitive idea of what a polyhedron really is, even though they cannot see it in space. |
|
In the film we see the five regular polyhedra pass through the plane, and we can watch the sections/polygons as they deform. This deformation is not easy to predict, since the sections depend on the way in which the polyhedra pass through. For example, if a cube approaches so that one of its faces is parallel to the plane, we are not surprised to see that the sections are squares. But if we cut a cube by a plane which goes through its center and is perpendicular to a diagonal, the intersection is a regular hexagon...which is perhaps less obvious! After having watched all of the polyhedra pass through the plane, Escher proposes some exercises for you. He shows you a sequence of polygonal sections in the plane and you must discover the polyhedron which is passing through, as though you were a flat lizard. Good luck with this exercise, which is not easy (as you will see). The method of sections has its limits, so we look for other methods... 5. Stereographic projectionHere is a second idea, which might seem bizarre but which will be extremely useful in what follows (when it is our turn to be "flat," confined to three dimensions while someone is trying to show us objects in his 4-dimensional world...). We learned how to project the sphere onto a plane by stereographic projection, and we have seen that even if this projection changes lengths it still gives a fairly exact picture of the geography of the Earth, especially if watch while the earth rolls on the plane. We could try do the same thing and roll the five polyhedra on a plane, projecting them stereographically. The problem is that we can't roll a cube because it is not round! So, we inflate the polyhedra like balls so that they become round. For example, we start by inscribing a cube inside a sphere. |
|
It is this method which is shown in the second part of this chapter. First we see the entire setup as seen by a three-dimensional being who sees everything: the polyhedron, the inflated polyhedron, the sphere, the projection onto the lizards' plane. Then we take the point of view of the flat lizards who can see only the projection. Escher finally appeals to our imagination to figure out which polyhedron we are seeing. The exercise is still not easy, but it does seem easier than using the method of slices. These exercises will be useful
for what follows.
Remember:
in a little while you will be in the position
of a poor 3-dimensional human incapable of seeing in the fourth
dimension! Someone
having the gift of being able to see in four dimensions will
try to show you what he sees, and he, too, will use slices and
projections. |
| To chapter 1 | To chapter 3 |