| 日本語 / русский / 繁 體中文 / Português / 简 体中文 / English / Español / Nederlands / العربية |
Chapitre 2 : la dimension troisM.C. Escher raconte les aventures de créatures de dimension 2 qui cherchent à imaginer des objets de dimension 3 |
| Vers chapitre 1 | Vers chapitre 3 |
1. Le présentateur |
|
M.C. Escher (1898-1972)
était un
artiste exceptionnel dont les œuvres séduisent
beaucoup les
mathématiciens. Ses gravures nous montrent des mondes
paradoxaux, des pavages aux symétries
stupéfiantes, des
perspectives infinies ; de quoi régaler les
mathématiciens
! Voir une biographie ici,
et le
site officiel
pour une grande collection de reproductions de gravures. J. S. Bach (1685-1750) est un autre artiste qui fascine les mathématiciens (entre autres !). Lui aussi nous montre des symétries étonnantes. Kurt Gödel (1906-1978) était un mathématicien qui a révolutionné la logique, exploitant lui aussi des symétries liant un tout et l'une de ses parties. Un livre remarquable "Bach Escher Gödel" explore ce lien profond qui unit ces trois personnages d'exception. |
|
L'une des gravures les plus célèbres de Escher s'intitule Reptiles. Prenez le temps de l'admirer ici car elle passe malheureusement trop vite dans le film. Sur une page d'un cahier de dessin, on voit un pavage dans lequel des lézards plats s'emboîtent à la perfection. |
|
C'est l'image d'un monde plat : les lézards qui vivent dans cette page ne connaissent que cette page, ils ignorent l'espace qui les entoure. Nous les voyons, nous savons que leur monde plat n'est qu'une page d'un cahier qui est situé dans notre espace, mais les reptiles plats l'ignorent. L'un de ces lézards a la chance d'échapper au plan et visite notre monde : on le voit en bas qui prend progressivement de l'épaisseur, qui grimpe sur un livre, emprunte une équerre en guise de pont qui le mêne sur un promontoire de forme dodécaèdrale, avant de redescendre et de reprendre sa position dans son monde plat, riche de sa nouvelle expérience, comme un explorateur qui aurait découvert un nouveau continent. La gravure incite à une
réflexion
philosophique : si ces
lézards ignorent l'existence du monde extérieur,
ne
sommes-nous pas dans la même situation ? N'existerait-il pas
un
monde
"extérieur" au nôtre, auquel nos sens ne nous
donnent pas
accès ? D'ailleurs, les allusions philosophiques abondent
dans
cette gravure. On y voit les quatre éléments qui
selon
Platon constituent le monde : l'eau dans le verre, l'air
expulsé
des narines du lézard, la terre dans le pot, le feu
évoqué par la boîte d'allumettes, et
même le
dodécaèdre qui représente la
quintessence, le
cinquième élément... Le papier
à cigarettes
de la marque Job est-il une allusion biblique ? |
|
| All
M.C. Escher
Works © 2008 The M.C. Escher Company,the Netherlands. All rights reserved. www.mcescher.com Used with permission. |
|
Le but de ce chapitre est de nous préparer à la quatrième dimension. Pour nous permettre d'envisager une quatrième dimension qui nous transcende, nous allons commencer à imaginer des stratagèmes pour expliquer à des lézards plats l'existence de la troisième dimension. Nous allons imaginer que nous sommes ce lézard élu du ciel (le philosophe ?, le mathématicien ?), qui a eu le privilège d'être autorisé à sortir de la page et de monter sur un dodécaèdre. Nous sommes dans l'espace de dimension 3, nous y voyons des objets, un pot, un livre, une équerre, un dodécaèdre, et notre mission est de "montrer ces objets" aux autres lézards qui ne peuvent pas les voir puisqu'ils sont dans un plan et qu'ils ne peuvent pas en sortir. 2. "Le plat pays" |
|
3. Les solides de PlatonQuels sont les objets de notre espace que nous allons "montrer" aux lézards plats ? Nous pourrions leur montrer un pot de fleurs ou un livre, mais nous allons rester dans l'allusion philosophique et leur montrer les cinq solides de Platon. |
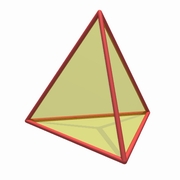 |
||||
| Tétraèdre | Octaèdre | Cube | Dodécaèdre | Icosaèdre |
|
Certains de ces objets nous sont familiers, comme le cube par exemple. D'autres se rencontrent parfois, comme le tétraèdre. D'autres sont plus rares et il faut être observateur pour les voir dans la nature. Prenez par exemple un icosaèdre,
avec ses
12 sommets et coupez les sommets comme sur la figure à
gauche.
On obtient un objet constitué de 20 hexagones et de 12
pentagones. Ces pentagones proviennent des 12 sommets qui ont
été coupés, et se trouvent sur les
faces d'un
dodécaèdre. Eh oui, on reconnaît
là un
ballon de
football... |
|
Ces objets sont des polyèdres, c'est-à-dire littéralement qu'ils ont plusieurs faces ! Notre but n'est pas ici d'entrer dans une théorie compliquée des polyèdres. Nous voulons simplement choisir cinq jolis objets dans l'espace et essayer de les montrer aux lézards. Expliquer à un lézard ce qu'est un ballon de football, en quelque sorte ! Il y a beaucoup de polyèdres (une infinité bien sûr) mais seuls cinq d'entre eux sont réguliers. Là encore, nous ne voulons pas entrer dans les détails de la définition de ce mot, mais observez que pour chacun de ces cinq polyèdres réguliers, toutes les faces sont du même type (par exemple, toutes les faces du dodécaèdre sont des pentagones réguliers, dont toutes les arêtes sont de même longueur), et que tous les sommets sont du même type (par exemple, de chaque sommet du cube, il y a exactement trois arêtes qui partent). Ces propriétés suffisent (presque) à caractériser les cinq objets que nous voulons montrer aux lézards. |
| Image | Nom | Faces | Sommets | Arêtes (longueur L) |
Surface | Volume |
| Tétraèdre | 4 | 4 | 6 | |||
| Octaèdre | 8 | 6 | 12 | |||
| Cube | 6 | 8 | 12 | |||
| Dodécaèdre | 12 | 20 | 30 | |||
| Icosaèdre | 20 | 12 | 30 |
|
Pour en savoir beaucoup plus sur les polyèdres, on peut consulter par exemple cette page, et pour en savoir beaucoup plus sur les cinq polyèdres réguliers, leur histoire et leurs symétries, on peut consulter cette page. Ces objets sont parmi les objets fétiches des mathématiciens car ils symbolisent le concept de symétries, qui n'est malheureusement pas détaillé dans le film. 4. Les sections |
|
Une première idée pour expliquer aux lézards ce qu'est un tétraèdre est de le couper en tranches. Cette idée est très ancienne et Edwin Abbott l'utilise largement dans son livre. C'est en quelque sorte ce qui est utilisé en tomographie, une technique d'imagerie médicale qui consiste à examiner le corps humain tranche par tranche et à reconstituer ensuite l'objet de dimension 3 à partir de ces sections successives. Lorsqu'un polyèdre se déplace dans l'espace et lorsqu'il rencontre le plan des lézards, l'intersection avec le plan est un polygone. Lorsque le polyèdre se déplace, le polygone se déforme et il finit par disparaître lorsque le polyèdre a fini de traverser le plan (les polyèdres seraient-ils le passe-muraille de Marcel Aymé ?). Les lézards ne voient que les polygones mais ils les voient de manière dynamique : ils peuvent voir comment ils se déforment. Avec un peu d'expérience, ils vont (peut-être !) finir par se faire une intuition de ce qu'est vraiment ce polyèdre qu'ils ne peuvent pas voir dans l'espace. |
|
Dans le film, on voit les cinq polyèdres réguliers qui traversent le plan et on montre les sections/polygones qui se déforment. Ce n'est pas facile car les sections dépendent de la manière dont les polyèdres traversent le plan. Par exemple, si un cube se présente de manière qu'une de ses faces soit parallèle au plan, il n'y a pas de surprise : les sections sont des carrés. Mais si on coupe un cube par un plan qui passe par son centre et qui est perpendiculaire à une diagonale, l'intersection est un... hexagone régulier et ceci est peut-être moins évident ?! Après avoir regardé tous les polyèdres traverser le plan, Escher vous propose des exercices. Il vous montre les sections polygonales dans le plan et vous devez deviner le polyèdre qui est en train de traverser, comme si vous étiez un lézard plat. Bonne chance pour cet exercice qui n'est pas facile, comme vous le verrez. La méthode des sections a donc ses limites et il nous faut trouver autre chose... 5. La projection stéréographiqueVoici une deuxième idée, qui peut paraître bizarre, mais qui sera extrêmement utile par la suite (lorsque ce sera notre tour d'être "plats", écrasés dans la troisième dimension, et qu'un élu tentera de nous montrer des objets dans son monde de dimension 4...). Nous avons appris à projeter la sphère sur un plan par projection stéréographique et nous avons vu que même si cette projection modifie les longueurs, elle donne cependant une idée assez précise de la géographie de la Terre, surtout si on la fait rouler sur un plan... Nous pourrions faire la même chose et faire rouler les cinq polyèdres sur un plan et les projeter stéréographiquement. Le problème est qu'on ne peut pas faire rouler un cube car il n'est pas rond ! Alors, on gonfle les polyèdres comme des ballons pour qu'ils deviennent ronds. Inscrivons par exemple un cube à l'intérieur d'une sphère. |
|
C'est cette méthode qui est montrée dans la deuxième partie de ce chapitre. D'abord, on montre l'ensemble vu par un être de dimension 3 qui voit tout : le polyèdre, le polyèdre gonflé, la sphère, la projection sur le plan des lézards. Puis, c'est à votre tour de prendre la place des lézards plats et de ne voir que la projection. Escher fait alors appel à votre imagination pour que vous puissiez deviner de quel polyèdre il s'agit. L'exercice n'est pas très facile non plus, mais il semble bien qu'il soit plus facile qu'avec la méthode des sections. Ces exercices seront utiles pour la suite.
Rappelez-vous
: d'ici peu,
vous serez dans la position d'un pauvre être humain de
dimension
3 incapable de voir dans la quatrième dimension ! Quelqu'un
ayant le don de voir dans la quatrième dimension fera des
efforts pour vous montrer ce qu'il voit. Il utilisera lui aussi des
coupes et des projections. |
| Vers chapitre 1 | Vers chapitre 3 |