Take a look at the contents of the film, or jump to the film's guide. 

Chapter 1 Dimension two. Hipparchus shows us how to describe the position of any point on Earth with two numbers...

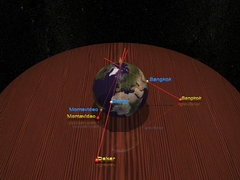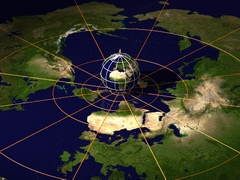
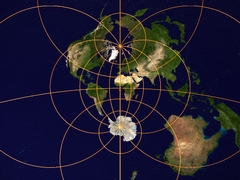
		...and explains the stereographic projection : how to draw a map of the world.

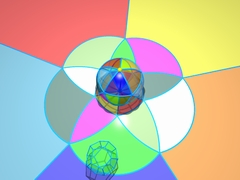
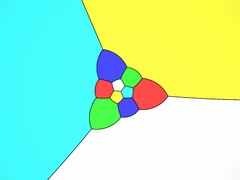
Chapter 2 Dimension three M.C. Escher talks about the adventures of two-dimensional creatures trying to imagine what three-dimensional objects look like.

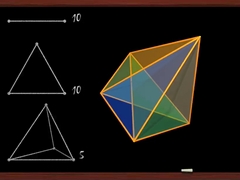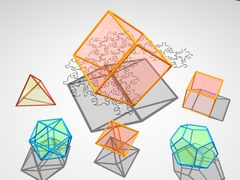
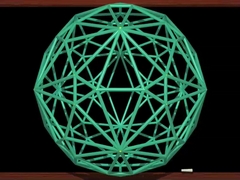
		Chapters 3 and 4 The fourth dimension Mathematician Ludwig Schläfli talks about objects that live in the fourth dimension...

..and shows a parade of four-dimensional polytopes, strange objects with 24, 120 and even 600 faces !

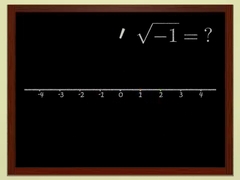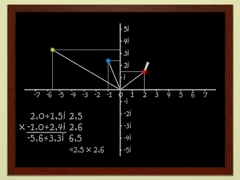
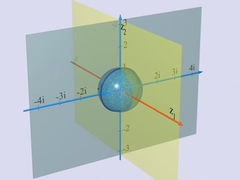
		Chapters 5 and 6 Complex numbers Mathematician Adrien Douady explains complex numbers. The square root of negative numbers made easy !

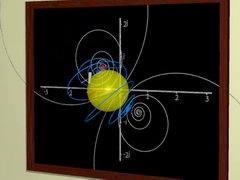
Transforming the plane, deforming images, creating fractal images...

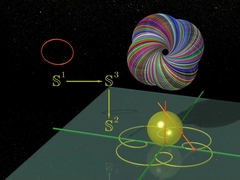
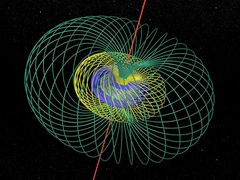
		Chapters 7 and 8 Fibration Mathematician Heinz Hopf explains his "fibration". Using complex numbers he constructs pretty patterns of circles in space.

Circles, tori... everything rotating in four-dimensional space.

		Chapter 9 Proof Mathematician Bernhard Riemann explains the importance of proofs in mathematics. He proves a theorem concerning the stereographic projection.

How can this film be used ?

The film can be enjoyed by anyone, provided the chapters are well-chosen.
There are 9 chapters, each 13 minutes long. Chapters 3-4, 5-6 and 7-8 are double chapters, but apart from that, they are more or less independent of each other.

One can of course sit down in front of a TV screen, or a computer, and watch the whole 117 minutes in one go!  Well, maybe there will be sequences that go too fast for you, or others that may be too elementary. This will depend on your interest, your prior knowledge on the subject, or simply on your mood of the moment !... However, one can also settle for some well-chosen chapters, and we have prepared some tips to help you get the best out of the film. For more information, go over to the detailed explanations pages, where you can find also short clips from the film..

In broad terms, the level of mathematics in the chapters increases gradually:

Chapter 1, dimension two, is very elementary. Secondary school students should be able to appreciate it, but we think that, even if you know already what meridians and parallels are, you will enjoy the spectacle of the Earth rolling like a ball ! (Look here).

Chapter 2, dimension three, is still elementary, but requires a bit of imagination, and it has some philosophical elements... There are even some exercises to check that you have understood. For explanations, additional information and references, one can consult this page

Chaptres 3 and 4 get us into the fourth dimension. This is of course more difficult, and maybe it will make your head spin ! In order to understand everything, don't hesitate to push the pause button on your remote, to watch these chapters several times, and to consult this page where you will find references to additional information. But even if you do not feel like making the effort to understand it all, you can always sit back and enjoy the pictures !

Chaptres 5 and 6, complex numbers, contain an introduction to, well... complex numbers. In France, complex numbers are taught in the final year of secondary school. We don't see this as a replacement for a classic course, but we think that these chapters could accompany such a course in a pleasant way. If you learned about complex numbers a long time ago, and you forgot most of it..., this could refresh your memory. If you know nothing about complex numbers, you should push the pause button as often as you like, and try to understand using the references that we propose. These chapters are the most "school-like" of the film. To thank you for your efforts, chapter 6 ends with an amazing deep zoom scene.

Chaptres 7 and 8 give you an introduction to the Hopf fibration, which is not taught in secondary school, and not even in the first years at university. This is certainly not beginner's stuff ! On the other hand, it is quite pretty and deserves to be understood. Everything is explained in the film, but of course, things may go a bit fast. Here also, the references that we provide can be useful in case you have trouble understanding... Good luck, and enjoy the show !

Finally, chapter 9 is a special one. It shows the proof of a theorem of geometry. This proof uses nothing above the level of secondary school, and we could very well have put this chapter right after chapter 1. Without proofs for theorems mathematics would not exist, and we wanted to make this very clear at the end of a film that is essentially about mathematical objects. (Look here).

Here are some possible choices :

Lower secondary school (ages 12-15) : 1 or 1-2 or 1-2-9
Higher secondary school (ages 16-18) : 1-2-(3-4)-9
Higher secondary school with science major : 5-6
University sciences student (lower cycle): 2-3-4-5 ou 5-6-(7-8-9)
University science student( higher cycle) : 7-8-(9)
General public : 1-2-3-4-(9)